常微分方程式を解くのに、わざわざルンゲクッタソルバを実装するまでもありません。
いや、実装したってたいしたことないです。解の安定性うんぬんを考えないのなら・・・・
さて。
SDのモデルから、微分方程式を立てるのは簡単です。立て方については、またそのうち書きます。急ぐ人はリンクるから、米国のエネルギー省のページでも見てがんがってください。
難しいのは正しく解くことです。数値解析でよいのです。数値解析なんて、戦前からあるんですから偉そうにやるこたぁないんです。ただ、計算機の科目のあまりにも基礎のところで出てくるので、習った人が修了する頃には忘れてしまうというだけのことです。日本史で縄文時代のことを忘れてしまいがちなのと同じですな。
さて、算数なら電卓、科学計算なら関数電卓。HP製プログラム電卓をお使いですか、そりゃすごいですなぁ。PCをお持ちなら、octaveはいかがでしょうか。
MATLABタダで使えりゃ苦労しませんがね。え?Mathmaticaが好き?知らんがな。
global m c k;
m=input("m= ");
c=input("c= ");
k=input("k= ");
function xdot=f(x,t);
global m c k;
xdot(1)=x(2);
xdot(2)=-(c/m)*x(2)-(k/m)*x(1);
endfunction
x0=[1;0];
t=linspace(0,25,100);
y=lsode("f",x0,t);
plot(t,y(:,1))
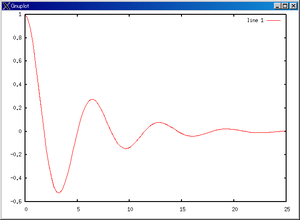
この「Octaveを使おう」のサンプルを実行したらこんなんでます~。
Cygwin-Xでoctave使えば最強です。もちろんいまどきのLinuxなら大抵はoctaveがポートされてるですから、それ使えばいいですが。
マスバネダンパー系の速度・加速度が、ストック・フローに化ければSDです。簡単でしょ?
りんくる:
Octaveを使おう
システムダイナミクスへのいざない(U.S. Department of Energy’s )
バージョンメモ:
Octave 2.1.73